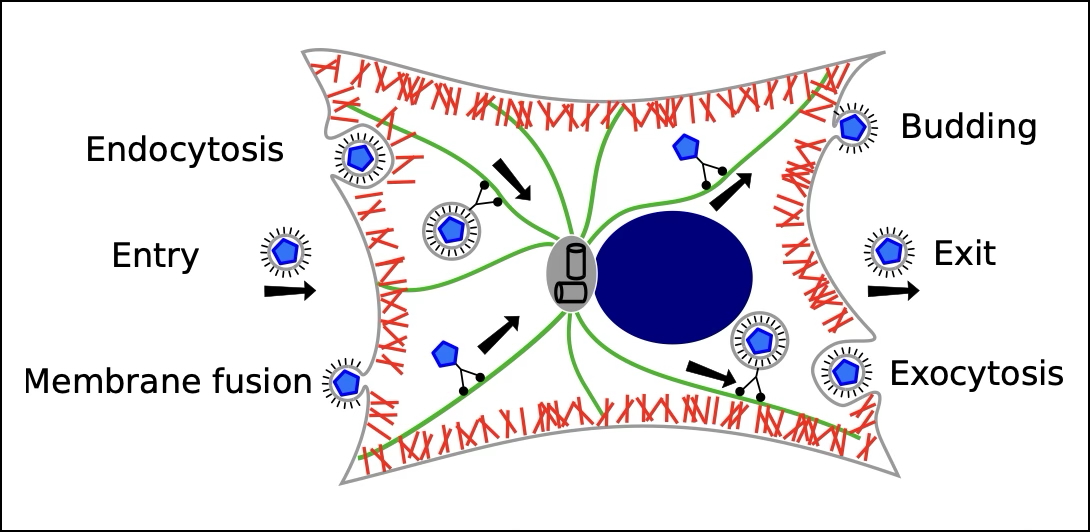
Many viruses enter cells via endocytosis. I contributed to understanding virus particle uptake by developing a continuum model that explores how virus shape affects uptake times (Frey et al., 2019) and incorporates stochasticity (Frey et al., 2019). This work included a collaborative study with the Spatz lab (MPI for Medical Research Heidelberg) (Wiegand et al., 2020) and a literature review on modeling virus replication and spread (Kumberger et al., 2016).
References
2020
-
Forces during cellular uptake of viruses and nanoparticles at the ventral side
Tina Wiegand , Marta Fratini , Felix Frey , Klaus Yserentant , and 11 more authors
Nat. Commun., Jan 2020
Many intracellular pathogens, such as mammalian reovirus, mimic extracellular matrix motifs to specifically interact with the host membrane. Whether and how cell-matrix interactions influence virus particle uptake is unknown, as it is usually studied from the dorsal side. Here we show that the forces exerted at the ventral side of adherent cells during reovirus uptake exceed the binding strength of biotin-neutravidin anchoring viruses to a biofunctionalized substrate. Analysis of virus dissociation kinetics using the Bell model revealed mean forces higher than 30 pN per virus, preferentially applied in the cell periphery where close matrix contacts form. Utilizing 100 nm-sized nanoparticles decorated with integrin adhesion motifs, we demonstrate that the uptake forces scale with the adhesion energy, while actin/myosin inhibitions strongly reduce the uptake frequency, but not uptake kinetics. We hypothesize that particle adhesion and the push by the substrate provide the main driving forces for uptake.
2019
-
Dynamics of particle uptake at cell membranes
Felix Frey , Falko Ziebert , and Ulrich S. Schwarz
Phys. Rev. E, Nov 2019
Receptor-mediated endocytosis requires that the energy of adhesion overcomes the deformation energy of the plasma membrane. The resulting driving force is balanced by dissipative forces, leading to deterministic dynamical equations. While the shape of the free membrane does not play an important role for tensed and loose membranes, in the intermediate regime it leads to an important energy barrier. Here we show that this barrier is similar to but different from an effective line tension and suggest a simple analytical approximation for it. We then explore the rich dynamics of uptake for particles of different shapes and present the corresponding dynamical state diagrams. We also extend our model to include stochastic fluctuations, which facilitate uptake and lead to corresponding changes in the phase diagrams.
-
Stochastic Dynamics of Nanoparticle and Virus Uptake
Felix Frey , Falko Ziebert , and Ulrich S. Schwarz
Phys. Rev. Lett., Feb 2019
The cellular uptake of nanoparticles or viruses requires that the gain of adhesion energy overcomes the cost of plasma membrane bending. It is well known that this leads to a minimal particle size for uptake. Using a simple deterministic theory for this process, we first show that, for the same radius and volume, cylindrical particles should be taken up faster than spherical particles, both for normal and parallel orientations. We then address stochastic effects, which are expected to be relevant due to small system size, and show that, now, spherical particles can have a faster uptake because the mean first passage time profits from the multiplicative noise induced by the spherical geometry. We conclude that stochastic effects are strongly geometry dependent and may favor spherical shapes during adhesion-driven particle uptake.
2016
-
Multiscale modeling of virus replication and spread
Peter Kumberger , Felix Frey , Ulrich S. Schwarz , and Frederik Graw
FEBS Lett., Feb 2016
Replication and spread of human viruses is based on the simultaneous exploitation of many different host functions, bridging multiple scales in space and time. Mathematical modeling is essential to obtain a systems-level understanding of how human viruses manage to proceed through their life cycles. Here, we review corresponding advances for viral systems of large medical relevance, such as human immunodeficiency virus-1 (HIV-1) and hepatitis C virus (HCV). We will outline how the combination of mathematical models and experimental data has advanced our quantitative knowledge about various processes of these pathogens, and how novel quantitative approaches promise to fill remaining gaps.